Contents

Disease Course Mapping

by Igor Koval

Disease Course Mapping in a nutshell

Neurodegenerative disease progresses over periods of time longer than the usual individual observations and with an important inter-individual variability. It directly prevents to straightforwardly disentangle a reference disease progression from its manifestation at an individual level.

For that purpose, we have developed a technique called Disease Course Mapping. Its aim is to estimate, both spatially and temporally, a unified spectrum of disease progression from a population. It directly allows to :

  • describe the average progression (along with its variability) of the biomarkers over the entire course of the disease

  • position any individual onto this map to precisely characterize the patients trajectory and predict his current and future stages

Longitudinal data Non-linear Mixed-effects model Description of disease progression Personalized staging & prediction

A picture is worth a thousand words

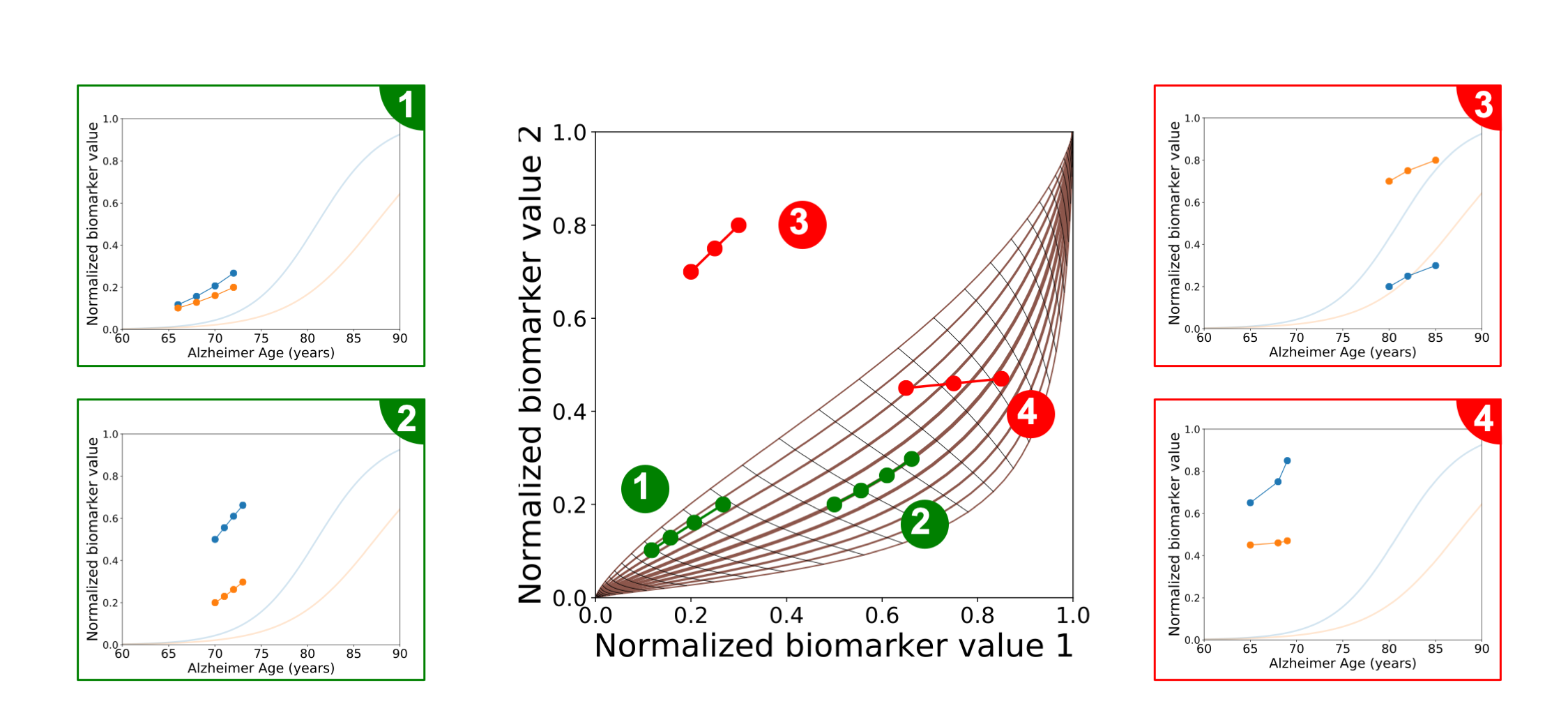
../../_images/trajectory_mapping.png

Fig. 2 Disease Course Mapping.

The central panel corresponds to the progression of two biomarkers (x and y axis) across the course of a neurodegenerative disease. Each curve represents the progression of these biomarkers over time, from [0, 0] to [1, 1]. The central curve corresponds to the average progression whose temporal representation is represented by the two idealized blue and orange curves on the four subpanels. Each point on the mapping corresponds to the value of two biomarkers measured at any visit. The repetition of visits therefore characterizes the positioning of a patient onto the disease progression spectrum. Its variability, reflected by the envelop around the average progression as well as the orientation of the curves that corresponds to the temporal trajectories, perfectly distinguishes likely individual progressions (green subpanels) from the one that do no appear in practice (red subpanels).

Model description

Input data

We here consider longitudinal data, i.e. patients with multiple visits along time, each corresponding to multiple observations : cognitive tests, neuropsychological assessments, medical imaging features, etc.

Attention

For the sake of clarity, in the following, we consider two biomarkers that have been normalized such that a value of 0 corresponds to normal (i.e. control) stages where 1 corresponds to pathological stages.

The aim of the model is to describe the progression of the biomarkers across the course of the disease. Let’s here assume that it corresponds to two idealized logistic curves as shown on Fig. 3. Given this average progression, how is it related to the observations of any new subject?

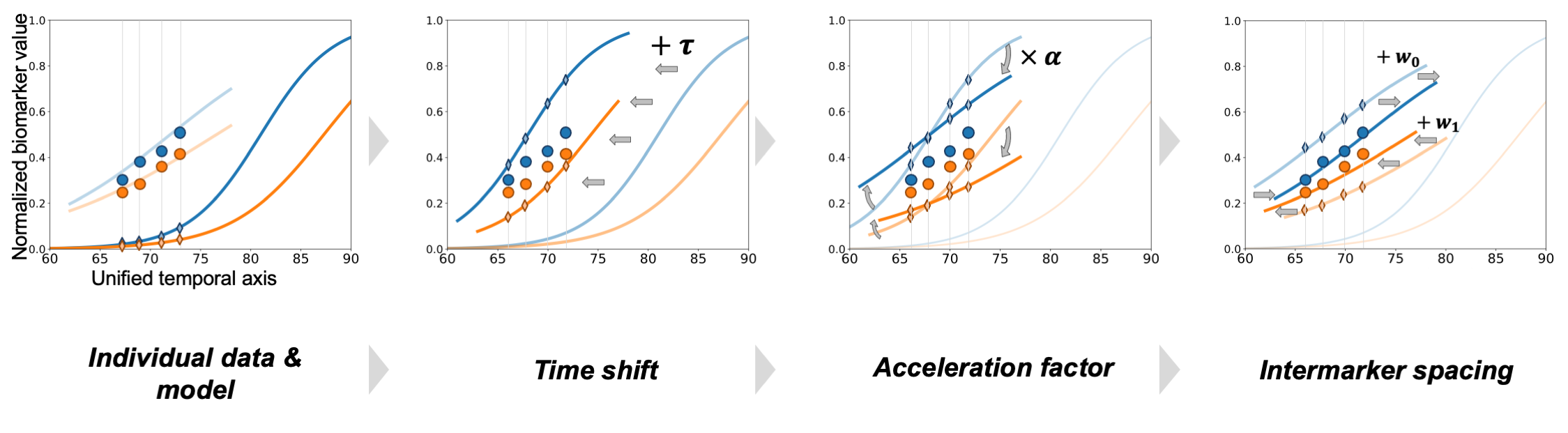
../../_images/model_explanation_1.png

Fig. 3 The individual trajectory corresponds to the average disease progression that has been (i) shifted thanks to the time shift, (ii) decelerated thanks to the acceleration factor, and, (iii) reordered thanks to the inter-marker spacing.

As shown on Fig. 3, we consider that the individual observations are variation of the average progressions in the sense that they derive from the mean biomarker trajectories, based on three subject-specific parameters :

The time-shift \(\tau\)

It shifts the disease onset by a given number of years. For instance, a time-shift of 7 delays the entire disease progression of 7 years. \(\tau > 0\) corresponds to disease progression that are later than the average one, while \(\tau < 0\) corresponds to earlier than average progression.

acceleration factor \(\alpha\)

It accelerates (\(\alpha > 1\)) or deccelerate (\(\alpha < 1\)) the overall disease progression, i.e. it changes the slope of the logistic curves

inter-marker spacing \(\omega\)

It accounts for the fact that the ordering of the event (i.e. biomarker progression) might differ within the population, therefore to each patient corresponds a given sequence of events described by the vector \(\omega\) that shifts each logistic curve. [Note: To ensure identifiability with the parameter \(\tau\), we enforce \(\sum \omega_k = 0\) ].

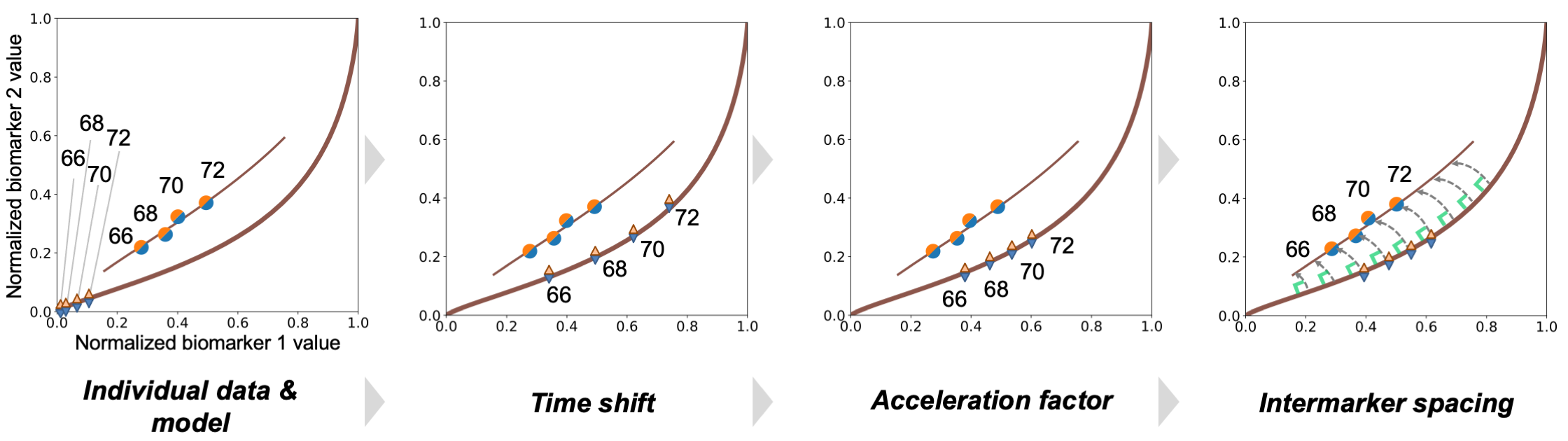
../../_images/model_explanation_2.png

Fig. 4 Variation of the average trajectory to the individual data in the Disease Mapping space.

The procedure that allows to derive the average trajectory can also be shown in the space of the biomarker, as shown on Fig. 4. It shows how the average progression is changed to fit the individual data - and vice-versa.

Though, a question still holds

How do we first estimate the average progression of the biomarkers from which any individual observations derive?

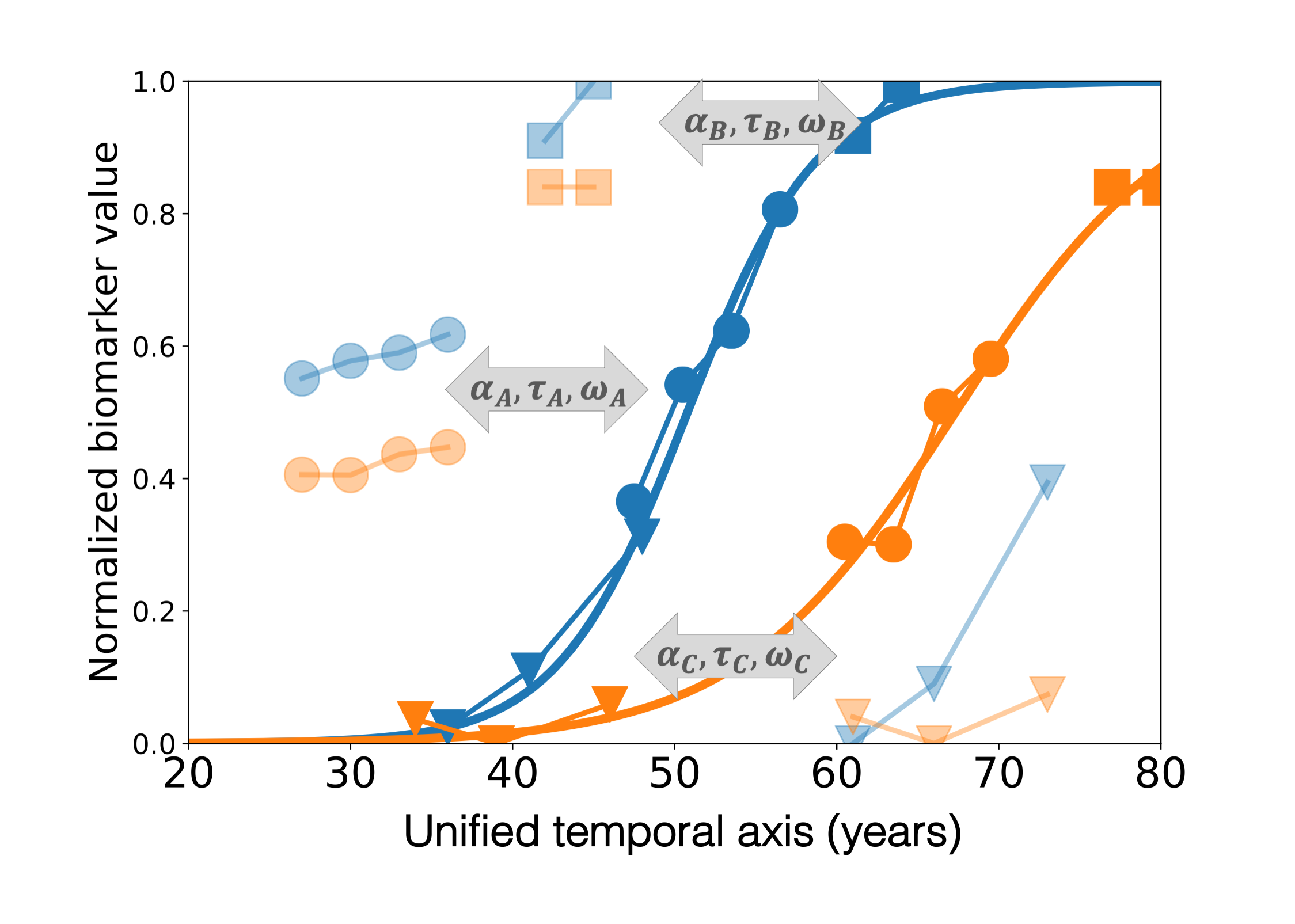
../../_images/calibration.png

Fig. 5 Model estimation

In practice, the average model of progression and the individual parameters are jointly estimated such that :

  • the variation of the mean trajectory fits the individual data (stochastic maximum likelihood estimation)

  • the individual parameters are considered as random variables whose mean corresponds to the average trajectory (mixed-effect model)

This procedure is sketched on Fig. 5 which shows that the average model corresponds to the recombination of the short-term individual measurements onto a long-term disease progression that spans different disease stages.

Then, once the model has been estimated, the estimation of the parameter of a new patient given this data corresponds to an optimization procedure, that under-the-hoods minimize the fit to the data and a regularization term over the individual parameters that follow normal distributions.

Note

As we derive a continuous model to fit the individual data, we can predict the future biomarkers values base on the patient observation as shown on Fig. 6. Such procedure can be done from a baseline visit only, and, has shown to be accurate (up to the noise level of the data) up to 5 years in advance.

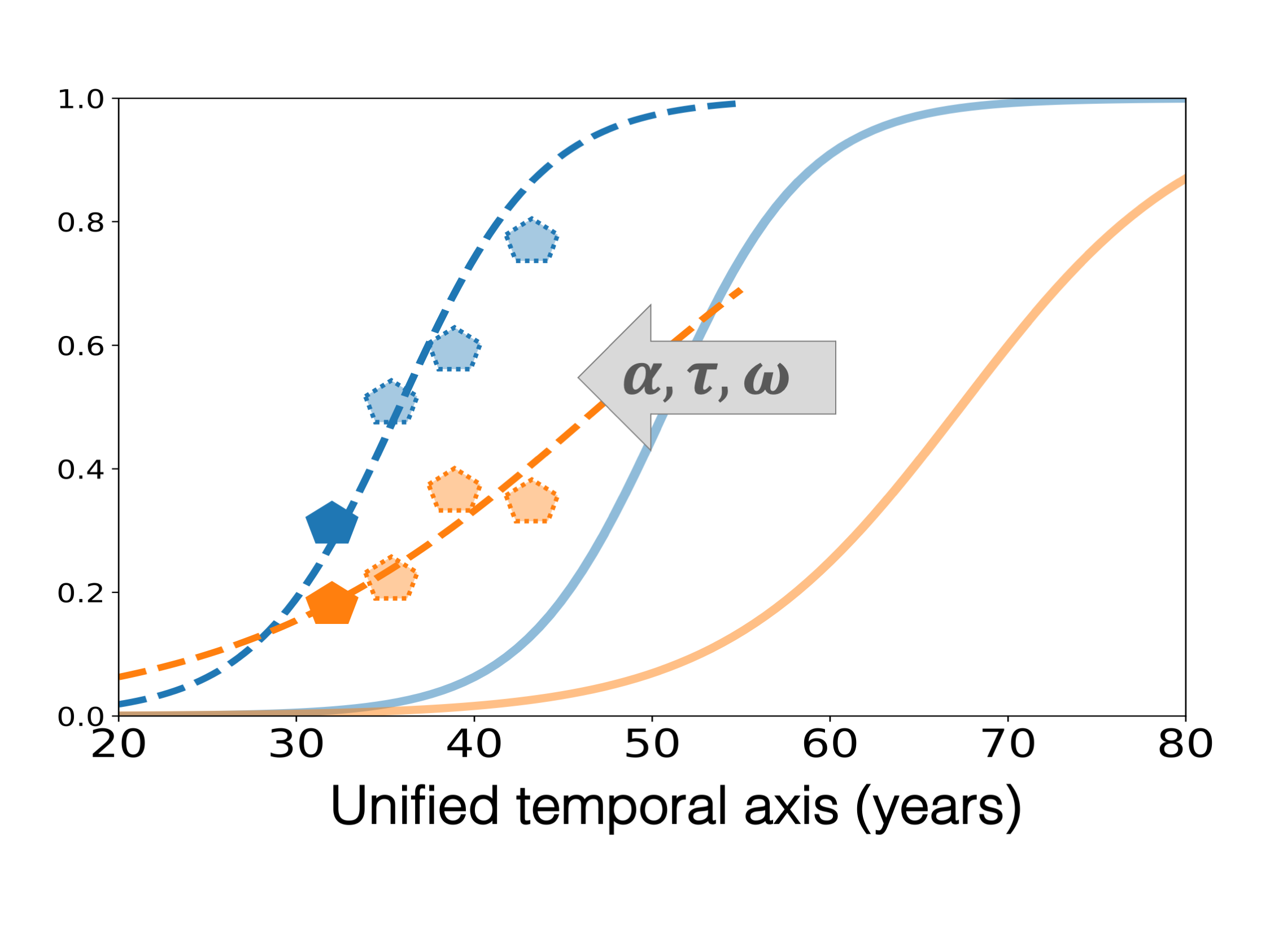
../../_images/prediction.png

Fig. 6 The personalization of the average trajectory to the individual data allows to predict the future values of the different biomarkers.

Disease Course Mapping as a software

Interested by this model? You want to test it on your own data?

It is made very easy thanks to the Leaspy software package. Give a look at the tutorials here.

Software Python package Open source Tutorials

References

More detailed explanations about the models themselves and about the estimation procedure can be found in the following articles :

  1. Mathematical Framework

  2. Model instantiations

  3. Applications

  4. Website & Code

Contacts

  • Igor Koval (See Contributors)

  • Stanley Durrleman http://www.aramislab.fr/

Event Based Model Gaussian Process Progression Model